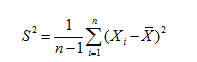2018考研數學三大綱已公布,社科塞斯考研網小編及時為大家分享2018考研數學三大綱,幫助大家備考考研數學,下面是2018年全國碩士研究生考試數學三考試大綱
考試科目:微積分、線性代數、概率論與數理統計
考試形式和試卷結構
一、試卷滿分及考試時間
試卷滿分為150分,考試時間為180分鐘.
二、答題方式
答題方式為閉卷、筆試.
三、試卷內容結構
微積分 約56%
線性代數 約22%
概率論與數理統計 約22%
四、試卷題型結構
單項選擇題選題 8小題,每小題4分,共32分
填空題 6小題,每小題4分,共24分
解答題(包括證明題) 9小題,共94分
微積分
一、函數、極限、連續
考試內容
函數的概念及表示法 函數的有界性、單調性、周期性和奇偶性 復合函數、反函數、分段函數和隱函數 基本初等函數的性質及其圖形 初等函數 函數關系的建立
數列極限與函數極限的定義及其性質 函數的左極限和右極限 無窮小量和無窮大量的概念及其關系 無窮小量的性質及無窮小量的比較 極限的四則運算 極限存在的兩個準則:單調有界準則和夾逼準則 兩個重要極限:
函數連續的概念 函數間斷點的類型 初等函數的連續性 閉區間上連續函數的性質
考試要求
1.理解函數的概念,掌握函數的表示法,會建立應用問題的函數關系.
2.了解函數的有界性、單調性、周期性和奇偶性.
3.理解復合函數及分段函數的概念,了解反函數及隱函數的概念.
4.掌握基本初等函數的性質及其圖形,了解初等函數的概念.
5.了解數列極限和函數極限(包括左極限與右極限)的概念.
6.了解極限的性質與極限存在的兩個準則,掌握極限的四則運算法則,掌握利用兩個重要極限求極限的方法.
7.理解無窮小量的概念和基本性質,掌握無窮小量的比較方法.了解無窮大量的概念及其與無窮小量的關系.
8.理解函數連續性的概念(含左連續與右連續),會判別函數間斷點的類型.
9.了解連續函數的性質和初等函數的連續性,理解閉區間上連續函數的性質(有界性、最大值和最小值定理、介值定理),并會應用這些性質.
二、一元函數微分學
考試內容
導數和微分的概念 導數的幾何意義和經濟意義 函數的可導性與連續性之間的關系 平面曲線的切線與法線 導數和微分的四則運算 基本初等函數的導數 復合函數、反函數和隱函數的微分法 高階導數 一階微分形式的不變性 微分中值定理 洛必達(L'Hospital)法則 函數單調性的判別 函數的極值 函數圖形的凹凸性、拐點及漸近線 函數圖形的描繪 函數的最大值與最小值
考試要求
1.理解導數的概念及可導性與連續性之間的關系,了解導數的幾何意義與經濟意義(含邊際與彈性的概念),會求平面曲線的切線方程和法線方程.
2.掌握基本初等函數的導數公式、導數的四則運算法則及復合函數的求導法則,會求分段函數的導數,會求反函數與隱函數的導數.
3.了解高階導數的概念,會求簡單函數的高階導數.
4.了解微分的概念、導數與微分之間的關系以及一階微分形式的不變性,會求函數的微分.
5.理解羅爾(Rolle)定理、拉格朗日( Lagrange)中值定理,了解泰勒(Taylor)定理、柯西(Cauchy)中值定理,掌握這四個定理的簡單應用.
6.會用洛必達法則求極限.
7.掌握函數單調性的判別方法,了解函數極值的概念,掌握函數極值、最大值和最小值的求法及其應用.
8.會用導數判斷函數圖形的凹凸性(注:在區間(a,b)內,設函數發f(x)具有二階導數.當fn(x)>0時,f(x)的圖形是凹的;當fn(x)<0時,f(x)的圖形是凸的),會求函數圖形的拐點以及水平、鉛直和斜漸近線,會描繪函數的圖形.
9.會描述簡單函數的圖形.
三、一元函數積分學
考試內容
原函數和不定積分的概念 不定積分的基本性質 基本積分公式 定積分的概念和基本性質 定積分中值定理 積分上限的函數及其導數 牛頓-萊布尼茨(Newton- Leibniz)公式 不定積分和定積分的換元積分法與分部積分法 反常(廣義)積分 定積分的應用
考試要求
1.理解原函數與不定積分的概念,掌握不定積分的基本性質和基本積分公式,掌握不定積分的換元積分法與分部積分法.
2.了解定積分的概念和基本性質,了解定積分中值定理,理解積分上限的函數并會求它的導數,掌握牛頓-萊布尼茨公式以及定積分的換元積分法和分部積分法.
3.會利用定積分計算平面圖形的面積、旋轉體的體積和函數的平均值,會利用定積分求解簡單的經濟應用問題.
4.了解反常積分的概念,會計算反常積分.
四、多元函數微積分學
考試內容
多元函數的概念 二元函數的幾何意義 二元函數的極限與連續的概念 有界閉區域上二元連續函數的性質 多元函數偏導數的概念與計算 多元復合函數的求導法與隱函數求導法 二階偏導數 全微分 多元函數的極值和條件極值、最大值和最小值 二重積分的概念、基本性質和計算 無界區域上簡單的反常二重積分
考試要求
1.了解多元函數的概念,了解二元函數的幾何意義.
2.了解二元函數的極限與連續的概念,了解有界閉區域上二元連續函數的性質.
3.了解多元函數偏導數與全微分的概念,會求多元復合函數一階、二階偏導數,會求全微分,會求多元隱函數的偏導數.
4.了解多元函數極值和條件極值的概念,掌握多元函數極值存在的必要條件,了解二元函數極值存在的充分條件,會求二元函數的極值,會用拉格朗日乘數法求條件極值,會求簡單多元函數的最大值和最小值,并會解決簡單的應用問題.
5.了解二重積分的概念與基本性質,掌握二重積分的計算方法(直角坐標、極坐標),了解無界區域上較簡單的反常二重積分并會計算.
五、無窮級數
考試內容
常數項級數的收斂與發散的概念 收斂級數的和的概念 級數的基本性質與收斂的必要條件 幾何級數與p級數及其收斂性 正項級數收斂性的判別法 任意項級數的絕對收斂與條件收斂 交錯級數與萊布尼茨定理 冪級數及其收斂半徑、收斂區間(指開區間)和收斂域 冪級數的和函數 冪級數在其收斂區間內的基本性質 簡單冪級數的和函數的求法 初等函數的冪級數展開式
考試要求
1.了解級數的收斂與發散、收斂級數的和的概念.
2.了解級數的基本性質及級數收斂的必要條件,掌握幾何級數及p級數的收斂與發散的條件,掌握正項級數收斂性的比較判別法和比值判別法.
3.了解任意項級數絕對收斂與條件收斂的概念以及絕對收斂與收斂的關系,了解交錯級數的萊布尼茨判別法.
4.會求冪級數的收斂半徑、收斂區間及收斂域.
5.了解冪級數在其收斂區間內的基本性質(和函數的連續性、逐項求導和逐項積分),會求簡單冪級數在其收斂區間內的和函數.
6.了解ex,sinx,cosx,ln(1+x),及(1+x)a的麥克勞林(Maclaurin)展開式.
六、常微分方程與差分方程
考試內容
常微分方程的基本概念 變量可分離的微分方程 齊次微分方程 一階線性微分方程 線性微分方程解的性質及解的結構定理 二階常系數齊次線性微分方程及簡單的非齊次線性微分方程 差分與差分方程的概念 差分方程的通解與特解 一階常系數線性差分方程 微分方程的簡單應用
考試要求
1.了解微分方程及其階、解、通解、初始條件和特解等概念.
2.掌握變量可分離的微分方程、齊次微分方程和一階線性微分方程的求解方法.
3.會解二階常系數齊次線性微分方程.
4.了解線性微分方程解的性質及解的結構定理,會解自由項為多項式、指數函數、正弦函數、余弦函數的二階常系數非齊次線性微分方程.
5.了解差分與差分方程及其通解與特解等概念.
6.了解一階常系數線性差分方程的求解方法.
7.會用微分方程求解簡單的經濟應用問題.
線性代數
一、行列式
考試內容
行列式的概念和基本性質 行列式按行(列)展開定理
考試要求
1.了解行列式的概念,掌握行列式的性質.
2.會應用行列式的性質和行列式按行(列)展開定理計算行列式.
二、矩陣
考試內容
矩陣的概念 矩陣的線性運算 矩陣的乘法 方陣的冪 方陣乘積的行列式 矩陣的轉置 逆矩陣的概念和性質 矩陣可逆的充分必要條件 伴隨矩陣 矩陣的初等變換 初等矩陣 矩陣的秩 矩陣的等價 分塊矩陣及其運算
考試要求
1.理解矩陣的概念,了解單位矩陣、數量矩陣、對角矩陣、三角矩陣的定義及性質,了解對稱矩陣、反對稱矩陣及正交矩陣等的定義和性質.
2.掌握矩陣的線性運算、乘法、轉置以及它們的運算規律,了解方陣的冪與方陣乘積的行列式的性質.
3.理解逆矩陣的概念,掌握逆矩陣的性質以及矩陣可逆的充分必要條件,理解伴隨矩陣的概念,會用伴隨矩陣求逆矩陣.
4.了解矩陣的初等變換和初等矩陣及矩陣等價的概念,理解矩陣的秩的概念,掌握用初等變換求矩陣的逆矩陣和秩的方法.
5.了解分塊矩陣的概念,掌握分塊矩陣的運算法則.
三、向量
考試內容
向量的概念 向量的線性組合與線性表示 向量組的線性相關與線性無關 向量組的極大線性無關組 等價向量組 向量組的秩 向量組的秩與矩陣的秩之間的關系 向量的內積 線性無關向量組的正交規范化方法
考試要求
1.了解向量的概念,掌握向量的加法和數乘運算法則.
2.理解向量的線性組合與線性表示、向量組線性相關、線性無關等概念,掌握向量組線性相關、線性無關的有關性質及判別法.
3.理解向量組的極大線性無關組的概念,會求向量組的極大線性無關組及秩.
4.理解向量組等價的概念,理解矩陣的秩與其行(列)向量組的秩之間的關系.
5.了解內積的概念.掌握線性無關向量組正交規范化的施密特(Schmidt)方法.
四、線性方程組
考試內容
線性方程組的克拉默(Cramer)法則 線性方程組有解和無解的判定 齊次線性方程組的基礎解系和通解 非齊次線性方程組的解與相應的齊次線性方程組(導出組)的解之間的關系 非齊次線性方程組的通解
考試要求
1.會用克拉默法則解線性方程組.
2.掌握非齊次線性方程組有解和無解的判定方法.
3.理解齊次線性方程組的基礎解系的概念,掌握齊次線性方程組的基礎解系和通解的求法.
4.理解非齊次線性方程組解的結構及通解的概念.
5.掌握用初等行變換求解線性方程組的方法.
五、矩陣的特征值和特征向量
考試內容
矩陣的特征值和特征向量的概念、性質 相似矩陣的概念及性質 矩陣可相似對角化的充分必要條件及相似對角矩陣 實對稱矩陣的特征值和特征向量及相似對角矩陣
考試要求
1.理解矩陣的特征值、特征向量的概念,掌握矩陣特征值的性質,掌握求矩陣特征值和特征向量的方法.
2.理解矩陣相似的概念,掌握相似矩陣的性質,了解矩陣可相似對角化的充分必要條件,掌握將矩陣化為相似對角矩陣的方法.
3.掌握實對稱矩陣的特征值和特征向量的性質.
六、二次型
考試內容
二次型及其矩陣表示 合同變換與合同矩陣 二次型的秩 慣性定理 二次型的標準形和規范形 用正交變換和配方法化二次型為標準形 二次型及其矩陣的正定性
考試要求
1.了解二次型的概念,會用矩陣形式表示二次型,了解合同變換與合同矩陣的概念.
2.了解二次型的秩的概念,了解二次型的標準形、規范形等概念,了解慣性定理,會用正交變換和配方法化二次型為標準形.
3.理解正定二次型、正定矩陣的概念,并掌握其判別法.
概率論與數理統計
一、隨機事件和概率
考試內容
隨機事件與樣本空間 事件的關系與運算 完備事件組 概率的概念 概率的基本性質 古典型概率 幾何型概率 條件概率 概率的基本公式 事件的獨立性 獨立重復試驗
考試要求
1.了解樣本空間(基本事件空間)的概念,理解隨機事件的概念,掌握事件的關系及運算.
2.理解概率、條件概率的概念,掌握概率的基本性質,會計算古典型概率和幾何型概率,掌握概率的加法公式、減法公式、乘法公式、全概率公式以及貝葉斯(Bayes)公式等.
3.理解事件的獨立性的概念,掌握用事件獨立性進行概率計算;理解獨立重復試驗的概念,掌握計算有關事件概率的方法.
二、隨機變量及其分布
考試內容
隨機變量 隨機變量分布函數的概念及其性質 離散型隨機變量的概率分布 連續型隨機變量的概率密度 常見隨機變量的分布 隨機變量函數的分布
考試要求
1.理解隨機變量的概念,理解分布函數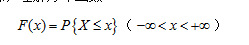 的概念及性質,會計算與隨機變量相聯系的事件的概率.
的概念及性質,會計算與隨機變量相聯系的事件的概率.
2.理解離散型隨機變量及其概率分布的概念,掌握0-1分布、二項分布B(n,p)、幾何分布、超幾何分布、泊松(Poisson)分布及其應用.
3.會求隨機變量函數的分布.
三、多維隨機變量的分布
考試內容
多維隨機變量及其分布函數 二維離散型隨機變量的概率分布、邊緣分布和條件分布 二維連續型隨機變量的概率密度、邊緣概率密度和條件密度 隨機變量的獨立性和不相關性 常見二維隨機變量的分布 兩個及兩個以上隨機變量簡單函數的分布
考試要求
1.理解多維隨機變量的分布函數的概念和基本性質.
2.理解二維離散型隨機變量的概率分布和二維連續型隨機變量的概率密度,掌握二維隨機變量的邊緣分布和條件分布.
3.理解隨機變量的獨立性和不相關性的概念,掌握隨機變量相互獨立的條件,理解隨機變量的不相關性與獨立性的關系.
4.掌握二維均勻分布和二維正態分布,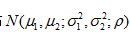 理解其中參數的概率意義.
理解其中參數的概率意義.
5.會根據兩個隨機變量的聯合分布求其函數的分布,會根據多個相互獨立隨機變量的聯合分布求其簡單函數的分布.
四、隨機變量的數字特征
考試內容
隨機變量的數學期望(均值)、方差、標準差及其性質 隨機變量函數的數學期望 切比雪夫(Chebyshev)不等式 矩、協方差、相關系數及其性質
考試要求
1.理解隨機變量數字特征(數學期望、方差、標準差、矩、協方差、相關系數)的概念,會運用數字特征的基本性質,并掌握常用分布的數字特征.
2.會求隨機變量函數的數學期望.
3.了解切比雪夫不等式.
五、大數定律和中心極限定理
考試內容
切比雪夫大數定律 伯努利(Bernoulli)大數定律 辛欽(Khinchine)大數定律 棣莫弗—拉普拉斯(De Moivre-Laplace)定理 列維—林德伯格(Levy-Lindberg)定理
考試要求
1.了解切比雪夫大數定律、伯努利大數定律和辛欽大數定律(獨立同分布隨機變量序列的大數定律).
2.了解棣莫弗—拉普拉斯中心極限定理(二項分布以正態分布為極限分布)、列維—林德伯格中心極限定理(獨立同分布隨機變量序列的中心極限定理),并會用相關定理近似計算有關隨機事件的概率.
六、數理統計的基本概念
考試內容
總體 個體 簡單隨機樣本 統計量 經驗分布函數 樣本均值 樣本方差和樣本矩x2分布 t分布F 分布 分位數 正態總體的常用抽樣分布
考試要求
1.了解總體、簡單隨機樣本、統計量、樣本均值、樣本方差及樣本矩的概念,其中樣本方差定義為
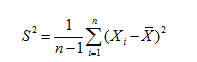
2.了解產生x2變量、t變量和f變量的典型模式;了解標準正態分布、x2分布、t分布和f分布的上側a分位數,會查相應的數值表.
3.掌握正態總體的樣本均值、樣本方差、樣本矩的抽樣分布.
4.了解經驗分布函數的概念和性質.
七、參數估計
考試內容
點估計的概念 估計量和估計值 矩估計法 最大似然估計法
考試要求
1.了解參數的點估計、估計量與估計值的概念.
2.掌握矩估計法(一階矩、二階矩)和最大似然估計法.
以上就是社科塞斯考研網小編為你整理的關于2018年考研數學三大綱的相關內容。希望對2018考研數學的同學們有所幫助!
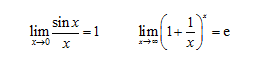
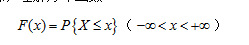 的概念及性質,會計算與隨機變量相聯系的事件的概率.
的概念及性質,會計算與隨機變量相聯系的事件的概率.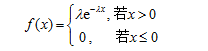
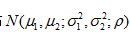 理解其中參數的概率意義.
理解其中參數的概率意義.